插補搜尋
介紹
插補搜尋（Interpolation Search）是一種搜尋演算法，適用於已排序的數據。它利用內插法的概念來估計目標值的位置，從而加快搜尋速度。與二分搜尋不同，插補搜尋假設數據是線性分佈的，並根據這一假設來計算中間位置（mid）。
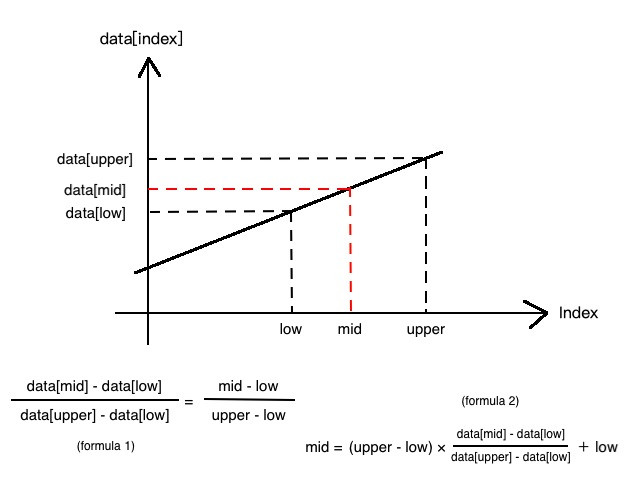
以上圖的公式 2 為例，當我們用要尋找的值(key)來算出 mid 的時候，比較 mid 是在右半部或是左半部。若是右半部則將 low 的邊界改為 mid，再重複一次圖上的公式 2，反覆運算後直到 mid 等於我們要尋找的值並輸出。反之亦然。
插補搜尋的步驟
- 初始化邊界：設置
low為數據的起始索引，upper為數據的結束索引。 - 計算中間位置：使用內插公式計算
mid： - 比較與調整邊界：
- 如果
data[mid]等於目標值key，則返回mid。 - 如果
data[mid]大於key，則將upper設為mid - 1。 - 如果
data[mid]小於key，則將low設為mid + 1。
- 如果
- 重複步驟 2 和 3，直到找到目標值或
low超過upper。
範例程式碼
以下是插補搜尋的 Python 範例：
python
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
def interpolation_search(data, key):
low = 0
upper = len(data) - 1
while low <= upper:
mid = int((upper - low) * (key - data[low]) / (data[upper] - data[low]) + low)
if mid < low or mid > upper:
break
if key < data[mid]:
upper = mid - 1
elif key > data[mid]:
low = mid + 1
else:
return mid
return -1
index = interpolation_search(data, 6)
if index >= 0:
print(index)
else:
print("找不到數值")優點與限制
- 優點：在數據均勻分佈的情況下，插補搜尋的效率比二分搜尋更高，平均時間複雜度為
。 - 限制：如果數據分佈不均勻，插補搜尋的性能可能會下降，最壞情況下時間複雜度為
。
插補搜尋適用於數據分佈均勻且已排序的情況，可以有效提高搜尋效率。
資源來源
Contributors
lucashsu95