DFS and BFS
DFS(深度優先搜索)
DFS 是一種用於遍歷或搜索樹或圖的算法。它從根節點(或任何其他節點)開始,沿着每個分支儘可能深地探索樹或圖,直到到達不能再前進的終點,然後回溯並探索另一個分支。
DFS 使用棧數據結構來存儲待訪問的節點。算法的主要步驟如下:
- 將起始節點壓入棧中。
- 重複以下步驟,直到棧為空:
- 從棧頂彈出一個節點。
- 對於彈出節點的每個未訪問過的相鄰節點:
- 將該節點壓入棧中。
- 將該節點標記為已訪問。
DFS 的時間複雜度為 O(V+E),其中 V 是節點數,E 是邊數。
BFS(廣度優先搜索)
BFS 是一種用於遍歷或搜索樹或圖的算法。它從根節點(或任何其他節點)開始,沿着每個分支逐層探索樹或圖,直到所有節點都被訪問過。
BFS 使用隊列數據結構來存儲待訪問的節點。算法的主要步驟如下:
- 將起始節點入隊。
- 重複以下步驟,直到隊列為空:
- 從隊列頭部取出一個節點。
- 對於取出節點的每個未訪問過的相鄰節點:
- 將該節點入隊。
- 將該節點標記為已訪問。
BFS 的時間複雜度為 O(V+E),其中 V 是節點數,E 是邊數。
BFS 和 DFS 的主要區別在於:
BFS先訪問當前層的所有節點,然後再訪問下一層的節點。DFS沿着每個分支儘可能深地探索樹或圖,直到到達不能再前進的終點,然後回溯並探索另一個分支。
例題
以下是使用 Python 實現的 DFS(深度優先搜索)和 BFS(廣度優先搜索)演算法的基本代碼。假設輸入的圖是通過邊的列表表示的,我們將使用字典來表示鄰接表。
輸入數據
我們將使用以下邊的列表來構建圖:
A B
A C
B D
B E
C F
C G
D H
F I
F J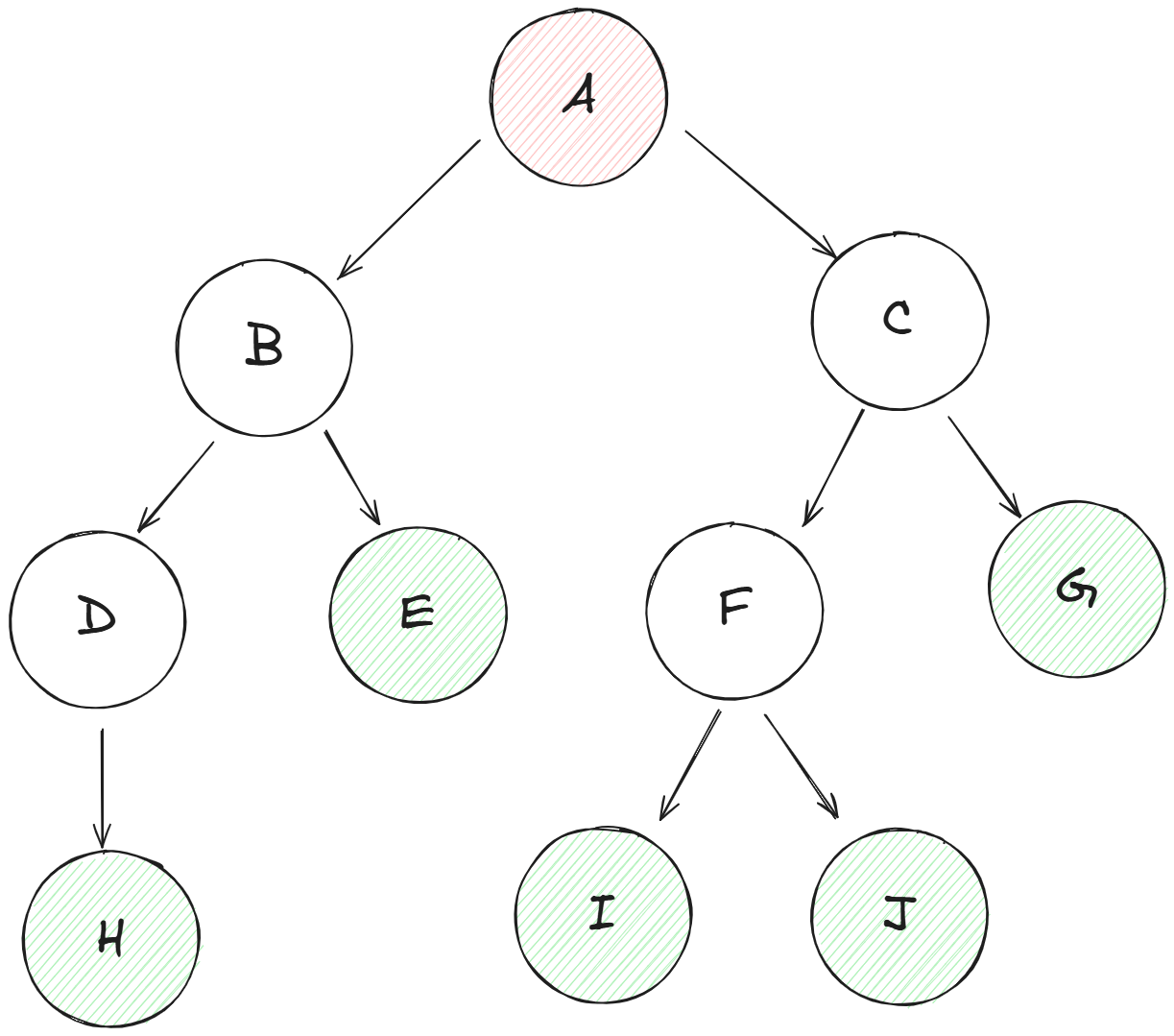
順變介紹一下
- 紅色的是根路徑(A節點)
- 綠色的是葉子,意思就是沒有子路徑的節點(E、G、H、I、J節點)
DFS 實現
python
def dfs(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start, end=' ')
for neighbor in graph[start]:
if neighbor not in visited:
dfs(graph, neighbor, visited)
# 構建圖的鄰接表
edges = [
('A', 'B'),
('A', 'C'),
('B', 'D'),
('B', 'E'),
('C', 'F'),
('C', 'G'),
('D', 'H'),
('F', 'I'),
('F', 'J')
]
graph = {}
for edge in edges:
graph.setdefault(edge[0], []).append(edge[1])
graph.setdefault(edge[1], []).append(edge[0]) # 因為是無向圖
print("DFS Traversal:")
dfs(graph, 'A')DFS Traversal:
A B D H E C F I J GBFS 實現
python
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
visited.add(start)
while queue:
vertex = queue.popleft()
print(vertex, end=' ')
for neighbor in graph[vertex]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
graph = {}
for edge in edges:
graph.setdefault(edge[0], []).append(edge[1])
graph.setdefault(edge[1], []).append(edge[0]) # 因為是無向圖
print("\nBFS Traversal:")
bfs(graph, 'A')BFS Traversal:
A B C D E F G H I J總結
- DFS 先深入到每一個分支,直到沒有更多的節點可以訪問,然後回溯。
- BFS 則是逐層訪問節點,確保當前層的所有節點都被訪問後,才會進入下一層。